1 简介
强化学习源于生物学的启发,即通过惩罚或者奖励来训练动物。几十年来,强化学习在控制方面都有着广泛的应用。而AlphaGo、AlphaGoZero的成功让强化学习大火。现在,强化学习已经成为自动驾驶等领域前沿研究的主流方法。另外,一些机器翻译、图片标题生成的研究中也尝试了强化学习。常见的强化学习方法包括:Q-learning、策略梯度(Policy gradient)、Actor-Critic。
2 一些基本概念
强化学习常见的应用场景中,包含有一个环境、一个代理(Actor)。Actor通过执行动作,改变状态,在这过程中可以从环境中得到一个奖励或者惩罚信号。一般我们会把时间分为T步,即把时间看成是离散的,当然如果是连续的时间,可以通过每隔一段时间采样信号,将连续时间转化为离散的信号。每个时间t,Actor执行一个动作![]() ,该时刻的状态为
,该时刻的状态为![]() ,到时间t=T时终止(terminal),时间[0,T]的整个过程叫做一个episode。例如:围棋中,Actor是下棋的AI,动作是选择下棋的位置,而状态是当前的棋子分布,整个棋局是一个episode。要注意,即使我们确定了动作,也不能确定下一个状态,因为我们不知道对手会怎么下。通常,为了方便学习,我们使用一个随机策略来选择要执行的动作,记为
,到时间t=T时终止(terminal),时间[0,T]的整个过程叫做一个episode。例如:围棋中,Actor是下棋的AI,动作是选择下棋的位置,而状态是当前的棋子分布,整个棋局是一个episode。要注意,即使我们确定了动作,也不能确定下一个状态,因为我们不知道对手会怎么下。通常,为了方便学习,我们使用一个随机策略来选择要执行的动作,记为![]() ,它是一个在动作空间的随机分布。
,它是一个在动作空间的随机分布。
为了进行学习,我们还需要一个奖励信号,通常用![]() 来表示,在围棋中,我们可以设置
来表示,在围棋中,我们可以设置![]() 表示在这一步中赢了,如果在这一步中输了则
表示在这一步中赢了,如果在这一步中输了则![]() ,而在其他步骤中,
,而在其他步骤中,![]() 。很明显,在结束之前的时间里,我们没有相应的奖励信号。因此,通常会使用一个长期的奖励信号来指导当前的步骤,
。很明显,在结束之前的时间里,我们没有相应的奖励信号。因此,通常会使用一个长期的奖励信号来指导当前的步骤,![]() 。这里的
。这里的![]() 是一个[0,1]之间的数字,表示奖励信号的衰减(discount factor)。当然这个长期奖励信号是一个随机变量,因为我们未来时间的动作、环境本身都存在着不确定性。把这个长期奖励信号的期望值记为
是一个[0,1]之间的数字,表示奖励信号的衰减(discount factor)。当然这个长期奖励信号是一个随机变量,因为我们未来时间的动作、环境本身都存在着不确定性。把这个长期奖励信号的期望值记为![]() ,由于这个值是未知的,我们通常使用它的估计值(state-value)
,由于这个值是未知的,我们通常使用它的估计值(state-value)![]() 。除了state-value之外,还有一个action-value,这个与state-value类似,记为
。除了state-value之外,还有一个action-value,这个与state-value类似,记为![]() ,它是给定状态s,以及动作a的情况下,长期奖励信号的估计值,而state-value是给定状态s下的长期奖励信号的估计。可以想象,如果我们每次都选择一个动作使得下一个状态的value最大,那么应该可以得到不错的结果。另外,
,它是给定状态s,以及动作a的情况下,长期奖励信号的估计值,而state-value是给定状态s下的长期奖励信号的估计。可以想象,如果我们每次都选择一个动作使得下一个状态的value最大,那么应该可以得到不错的结果。另外,![]() 通常用来表示时间差误差(temporal-difference error),实际上是用对
通常用来表示时间差误差(temporal-difference error),实际上是用对![]() 的误差估计(
的误差估计(![]() )。
)。
PS:在RL:an introduction一书[1]中作者建议使用大写字母来表示随机变量(如:Q, S),用小写字母来表示随机变量的具体取值(如:q, s)。
3 Q-learning
Q-learning算法学习一个action-value函数。通过估计某个状态s下,执行某个动作a后的奖励信号期望值。已经有文献证明对于任意finite Markov decision process (MDP)[2],Q-learning算法可以得到最优解。在学习到Q函数以后,每次都选择执行Q值最大的动作。
当然,在学习过程中,如果策略是每次都选择Q值最大的动作,那么学习过程就只会选择一些已经探索过的局面,而无法学习到新的东西。这个很像一些棋类AI,每次都是相同的套路。这个问题被称为exploration-exploitation problem,即每次是探索新的情况还是要利用已经学习到的知识。而在Q-learning的学习中,为了兼顾探索性,通常会使用一些随机的策略,包括:
1)![]() :以
:以![]() 的概率选择Q值最大的动作,以
的概率选择Q值最大的动作,以![]() 的概率随机选择一个动作。
的概率随机选择一个动作。
2)Boltzmann Policy:选择动作a的概率服从![]() 。这里的
。这里的![]() 是一个参数,值越大,那么越倾向于探索新的情况,通常会选择让它在学习过程中不断衰减。
是一个参数,值越大,那么越倾向于探索新的情况,通常会选择让它在学习过程中不断衰减。
Q-learning的参数更新函数为:

Q-learning并没有等到整个episode结束以后再学习,而是通过当前时间的奖励信号,以及下一个时刻的最大Q值来进行参数更新。除了terminal步骤以外,其他步骤都利用了已经学习到的Q函数。
Q-learning最大的缺点就是学习速度慢,另外学习过程中policy也难以确定,学习过程中的policy与最终使用的policy也存在不一致性。当action空间很大的时候,函数的维度会很高。
3.1 SARSA
SARSA与Q-learning非常像,它的学习过程为:
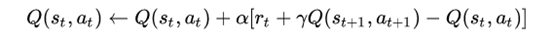
它们其实都是利用了![]() 。不过Q-learning学习过程中下一个步骤的动作不是确定的,它的一个样本是<s,a,r,s’>而SARSA中下一个步骤中的动作是确定的,它的一个样本是<s,a,r,s’,a’>(这里用s’,a’表示下一个时刻的状态与动作)。SARSA使用已经发生的动作序列进行学习,严格按照policy来选择动作(例如Boltzmann Policy),因此被称为on-policy algorithm。而Q-learning中的
。不过Q-learning学习过程中下一个步骤的动作不是确定的,它的一个样本是<s,a,r,s’>而SARSA中下一个步骤中的动作是确定的,它的一个样本是<s,a,r,s’,a’>(这里用s’,a’表示下一个时刻的状态与动作)。SARSA使用已经发生的动作序列进行学习,严格按照policy来选择动作(例如Boltzmann Policy),因此被称为on-policy algorithm。而Q-learning中的![]() 实际上并不一定非要执行动作,所以也可以从已经发生的episode中学习,因此被称为off-policy algorithm。以围棋为例,off-policy algorithm可以从以前下过的棋局、其他人下过的棋局学习知识;而on-policy algorithm只能边下棋边学习。
实际上并不一定非要执行动作,所以也可以从已经发生的episode中学习,因此被称为off-policy algorithm。以围棋为例,off-policy algorithm可以从以前下过的棋局、其他人下过的棋局学习知识;而on-policy algorithm只能边下棋边学习。
4 Policy gradient
假设策略的参数为![]() ,通过设定一个策略的性能指标
,通过设定一个策略的性能指标![]() ,Policy gradient通过J的梯度来学习最优策略。
,Policy gradient通过J的梯度来学习最优策略。
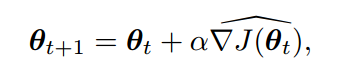
其中Actor-Critic也是Policy gradient中的一种方法,它同时学习了一个policy与value函数,这里的actor指的是policy,即动作执行者,而critic指的是value函数,即对于某个状态的评价。
Q-learning与SARSA学习中使用的policy与最终使用的policy存在不一致性,相对而言,policy gradient不存在策略退化问题,因为它学习到的策略正是最终使用的策略。
一般来说,policy的性能指标可以选择为:
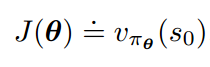
即在初始状态下,使用这个策略能够达到的长期奖励信号期望值。以围棋为例,这好比说,使用该策略的胜率有多高。这里要注意v是一个随机变量的期望值。
通过一些推导,可以得到:
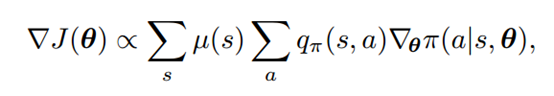
这里![]() 是在使用策略
是在使用策略![]() 的情况下,到达状态s的概率。
的情况下,到达状态s的概率。
推导过程分为2步,首先:
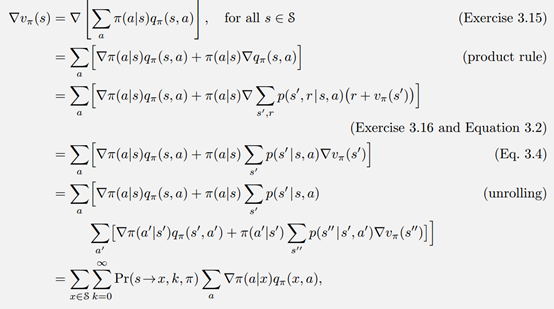
这里的![]() 表示在该策略下,在第k步从状态s转移到x的概率。然后,
表示在该策略下,在第k步从状态s转移到x的概率。然后,
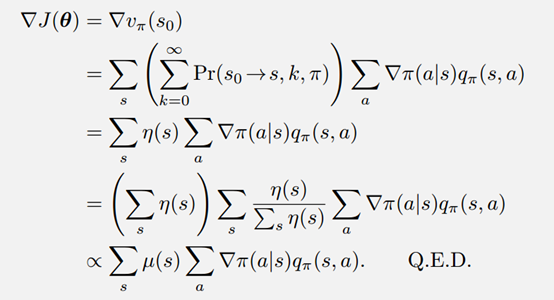
整个推导过程主要在于使用状态、动作的概率将期望的计算公式展开。
算法REINFORCE方法使用蒙特卡洛采样来估计。
由于
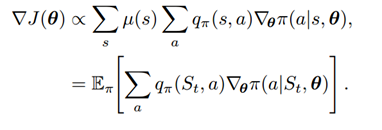
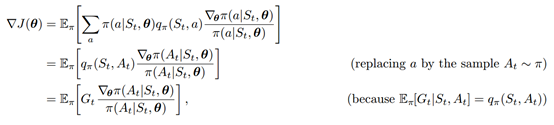
这里的![]() 表示return,
表示return,![]() ,可以看成是
,可以看成是![]() 的采样值。因此,REINFORCE的更新公式为:
的采样值。因此,REINFORCE的更新公式为:
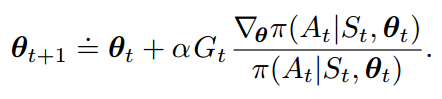
利用![]() 的导数性质,以及加上对于衰减因子的考虑。更新公式可以简化为:
的导数性质,以及加上对于衰减因子的考虑。更新公式可以简化为:
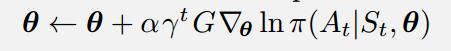
进一步,这里可以使用一个编程技巧,即使用![]() 作为损失函数可以得到等价的更新公式。
作为损失函数可以得到等价的更新公式。
REINFORCE with baseline: 在policy gradient的更新公式中,将action-value减去一个baseline值,可以得到一个更加一般化的更新公式:
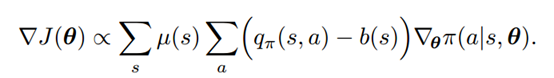
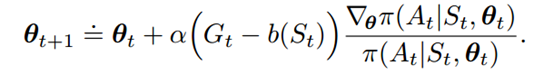
只要basline值b(s)与a无关,那么式子依然是有效的,因为从平均结果来看:
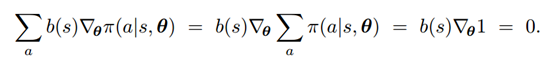
所有的action的概率之和为1,因此这个式子为0。也就是说加入一个baseline对于梯度的计算没有影响。但是实验表明,加入baseline可以降低variance,使得训练过程更加有效。
如果将baseline看成对于state-value的估计![]() (w表示state-value函数的参数),那么相应的算法变为:
(w表示state-value函数的参数),那么相应的算法变为:

5 Actor-critic
上面这个算法只是将state-value看成是一个baseline,而actor-critic对于state-value的利用更加彻底,使用一种自举(boostrapping)的方式来利用state-value函数。REINFORCE with baseline方法使用蒙特卡洛采样的方式,学习更慢(通常会产生的估计variance很大),而且很难进行在线学习(例如棋类AI边下棋边更新参数,而不是等到下完再进行更新)。而actor-critic则克服了这些缺点。
Actor-critic的更新式子为:
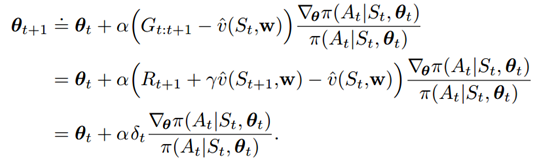
具体的更新算法为:

现在很多模型都是使用两个神经网络分别作为state-value以及policy函数,由于它们的输入都是状态S,因此有时会设定两个神经网络共享底层部分,即参数w与![]() 有一部分是重叠的。
有一部分是重叠的。
值得注意的是本文的算法都只举了one-step的例子,实际上它们都可以推广到multi-step中,例如把![]() 改为:
改为:
![]()
6 优化算法
DeepMind针对强化学习提出了很多的优化算法,目前最好用的PPO,在此之前还有A3C、TRPO。这些算法都是异步更新算法,可以同时运行多个actor来更新参数,以便加速训练。PPO提出一种Clipped surrogate objective,对reward进行裁剪,使得训练过程更加稳定。
7 总结
强化学习非常适合于一些反馈信号有延迟的场景。一些不可微的指标也可以直接当成reward来学习。因此强化学习适用于很多应用场景,有着其他算法不可比拟的优点。
参考:
[1] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction. http://incompleteideas.net/book/bookdraft2017nov5.pdf
[2] https://en.wikipedia.org/wiki/Markov_decision_process
[3] http://rll.berkeley.edu/deeprlcourse/f17docs/lecture_5_actor_critic_pdf.pdf
大量强化学习算法的Keras代码:
https://github.com/keras-rl/keras-rl
DeepMind公开的强化学习代码(基于tensorflow,包括PPO):